Earthquake relocation – As of February 2014, the Croatian Earthquake Catalogue (CEC) lists 9201 earthquakes in the greater Mt. Velebit region (blue rectangle in Fig. a1), of which 1357 are located in the Mt. Velebit area as defined by a red rectangle in Fig. a1. More than 2/3 of them occurred in the last 10 years, which means that a lot of digital data exist. Routine locations were often done using only Croatian data, or data from the neighbouring countries which were available at the time of the bulletin preparation. Furthermore, large majority of locations were computed using average regional velocity models which do not adequately represent individual travel-times. The problem of inadequate travel-time curves in a geologically and tectonically complicated region as this one may be solved either by constructing accurate 3-D velocity models of the crust and upper mantle, or by using a simple and reasonable reference model, and iteratively determine and apply station corrections for each station–phase–epicentral region combination. We therefore propose to:
- Carefully (re)analyse available digital seismograms that were not included in routine analyses (primarily those from Slovenia and Italy) and/or add missing data from respective bulletins;
- Divide the study area into small non-overlapping cells (e.g. 20 km x 20 km).
- Perform a cycle of earthquake location–station correction determinations for all stations and all phases, computing average corrections (for each station and phase) cell by cell, according to the epicentral coordinates of respective earthquakes. Repeat until station corrections and locations stabilize.
Fault plane solutions (FPS) – Methods for the first motion polarity determination of FPS are well known, with a number of established programs for their computation. Here we’ll use a program which utilises, besides the polarities themselves, also a priori information on the sharpness and prominence of the first motion, as well as ratios of observed P, SV and SH waves. The use of ratios significantly reduces ambiguity of solutions caused by insufficient sampling of the focal sphere (e.g. Snoke, 2009; Havskov and Ottemöller, 2010). We expect that we’ll be able to confidently determine FPS for most events in the Mt. Velebit area with magnitudes as low as 2.3–2.5, once the Velebit-net is set up and fully operational.
Receiver functions (RF) – The basis of the receiver function (RF) method is the fact that seismic waves get converted to different phases at the sharp impedance contrasts. More specifically, for the crustal exploration we seek to exploit steeply incident teleseismic P-to-S converted waves, which are mainly recorded on the horizontal components. Although both bulk-sound (P) and shear (S) waves can be used as the source of the converted waves P to S conversions are usually preferred in the crustal exploration because of the shorter wavelengths, which is more appropriate for mapping small-scale structures in the crust. Converted phases coming shortly after the first arrival of the P wave are usually obscured by the source complexities and other arrivals originating near the source. To isolate effects of local structures recorded on horizontal components these components are deconvolved with the vertical component (Vinnik, 1977; Langston, 1979). The resulting waveform is termed the ‘receiver function’ and represents the transfer function of the medium beneath the recording station. Each peak or through in the receiver function represents phase conversion at the particular impedance contrast. By measuring arrival times and amplitudes of these peaks we can reconstruct crustal structure under the seismic station. In order to use the full range of information contained in the RFs we need to use waveform inversion. Product of the RF waveform inversion is the 1D depth model of seismic velocities beneath the station along with the information about the anisotropy and structural dipping (e.g Savage, 1998; Tkalčić et al., 2006; Piana Agostinetti and Maliverno, 2010; Stipčević et al., 2011; Bodin et al., 2012).
In this project our aim is to use receiver functions analysis to map major discontinuities in the crust and upper mantle. We will use both waveform inversion and raytracing to create 1D velocity models beneath each station in the proposed Velebit-net seismic array. Based on the experience from previous measurements in the area (Stipčević, 2012) we expect that around 100 high quality teleseismic events can be recorded in each year of the project, which will provide solid data set for estimation of the subsurface structure.
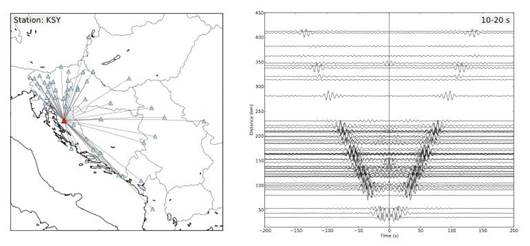
Ambient noise tomography – Theoretical studies have shown that an estimate of the Green’s function between two seismic recorders can be retrieved from cross-correlation of diffuse wavefield records (e.g. Weaver and Lobkis, 2001; Snieder, 2004; Wapenaar, 2004). In practice this means that by cross-correlating long term recordings from two stations we are amplifying coherent waveforms recorded at both stations. Ambient noise tomography uses the measurements of the dispersive part of the estimated Green’s function (coherent broadband Rayleigh wavetrains) at an array of seismic stations to obtain information on the subsurface elastic structure of the Earth.
Fig. c1. Example of preliminary analyses and estimated Green’s functions (bandpass filtered between 10 and 20 s) for paths between the station KSY located in the Velebit region (red triangle) and seismic stations (blue triangles) in the greater Dinaric area.
Group velocities are measured through arrival times of the highest amplitude on the envelope of the bandpass filtered seismograms. After obtaining traveltimes between station pairs in the array we will proceed to generate tomographic maps for each period. The usable period range depends on the spacing between recorders and in the case of the Velebit-net we estimate usable range to be from 1 to 20 seconds. This period range will allow us to probe crust up to 25 km depth. The processing of data in order to obtain estimate of the Green’s functions will closely follow procedure described in the papers by Bensen et al. (2007) and Young et al. (2013) with the addition of using prewhitening in order to reduce influence of local seismicity on cross-correlations.
Joint inversion of receiver functions and surface wave dispersion data – Receiver functions and surface wave dispersion data form a natural pair which makes ideal platform for joint inversion. By using both data sets in conjunction we can achieve higher level of constraint than it would be possible if data sets were used separately. This is possible because RFs are sensitive to velocity contrasts but lack sensitivity to absolute velocity while surface wave dispersion data constrain absolute shear wave velocity properties of the volume they sample but cannot constrain sharp gradients (e.g. Julia et al., 2000; Bodin et al., 2012). After obtaining both receiver function and ambient noise dispersion measurement we will invert both data sets jointly in order to provide further constraints on the seismic structures beneath Mt. Velebit area.
Crustal investigations in the Bayesian framework – In the recent years new inversion principle based on the Bayesian reasoning has overtaken geophysical community by storm. Early works of Maliverno (2000, 2002) have shown that a probabilistic Bayesian inference is ideally suited for the highly non-unique and non-linear geophysical inverse problems. In Bayesian parameter estimation process the model parameter space is sampled using the prior probability values and the likelihood function of the data through Bayes rule. In the second stage of this process we compare competing models that have different parameterisation and only retain ones that satisfy certain criteria which in the end gives posterior distribution over the model space. In this approach model parameters, including the level of data noise, are treated as unknowns and are represented by a probability distribution function that depends on known prior information and information provided by the data. This approach is often referred to as being transdimensional because the number of parameters (i.e. number of unknowns) changes during the inversion. Bayesian transdimensional method has been applied to the variety of seismological problems including receiver functions (Piana Agostinetti and Maliverno, 2010; Bodin et al., 2012a), ambient noise tomography (Bodin and Sambridge, 2009; Bodin et al., 2012b; Young et al., 2013) and dispersion data (Bodin et al., 2012a; Dettmer et al., 2012).
In this project we will use algorithms based on Bayesian transdimensional inversion method in order to infer crustal velocity structure. We will apply this inversion method to the receiver functions, ambient noise tomography and to joint inversion of RFs and surface wave dispersion data in order to create detailed 3D maps of the seismic structure in the proposed study area.
Attenuation – Attenuation is a propagation effect, which combined together with source and site effects, determines the shape and the frequency content of the earthquake seismogram. In order to explore one of these effects, we have to remove the other two. Therefore knowledge of attenuation is important for determining seismic source parameters, good quality modelling and inversions, and estimating seismic hazard. Furthermore, attenuation is more sensitive to temperature changes and fluid content in rocks than are seismic velocities: this makes it valuable when inferring about the structure and geodynamics of the area.
One of the most frequently used methods to estimate attenuation is the measurement of the quality factor QC based on the coda waves attenuation rate. Coda waves are incoherent waves caused by the scattering of the elastic waves on the heterogeneities in the Earth’s interior. They are seen as the wave train following the direct S-wave phases in a local earthquake seismogram. QC describes the total attenuation, which includes both elastic energy conversion into heat (intrinsic absorption) and energy redistribution of waves scattered on the heterogeneities (scattering). We will use the single backscattering theory proposed by Aki and Chouet (1975) to estimate frequency dependence of coda-Q from local earthquakes, whereas its dependence on the lapse-time will hint at the attenuation properties at different depths. This approach is useful for observing heterogeneities in the lithosphere on the scale of 0.1–10 km (Sato and Fehler, 1998) in a large volume that can sample medium at depths well into the uppermost mantle.
To estimate attenuation of body waves in the upper crust we will apply the coda normalization method in order to obtain attenuation of direct S-waves as proposed by Aki (1980) and extended for direct P-waves by Yoshimoto et al. (1993).
In both methods we use only recordings of local earthquakes. We will analyse quality factors dependence on lapse time, frequency, azimuth and earthquake source depth. This will enable us to make good quality moment magnitude estimations and give us additional information about the structure of the studied area.
Seismic anisotropy – Seismic anisotropy results from the preferred orientation of features of different scales due to present or past large-scale geodynamical processes within the Earth's deep interior. Thus, measurements of seismic anisotropy can provide information on lithospheric deformation, mantle flow directions and plate tectonics. In the last couple of decades, analysis of teleseismic SKS splitting has become a powerful and widely accepted technique for detecting such anisotropic structures in the Earth’s crust and upper mantle. In the project we shall determine splitting parameters (fast polarization direction and delay time) using the method described by Silver and Chan (1991). Results of the study should provide constrains for modelling geodynamical processes occurring in the region and enhance understanding of Earth’s crust and upper mantle structure. Methods for estimation of velocity anisotropy within hypocentral volumes using differential travel-times and travel-paths of local phases (primarily Pg) are described in Lokmer and Herak (1999), Herak et al. (2003) and Herak et al. (2009).
Geology and seismotectonics – Construction of local- to regional-, shallow- to crustal-scale geological cross-sections will be performed using standard methods and techniques in structural geology and geological mapping, like the dip-domain technique (e.g. Gill, 1953) and the method of circular arcs (e.g. Busk, 1929), with projection of surface structural data into the subsurface. This data will be supplemented with data obtained from available reflection seismic sections and deep exploration wells, all integrated into the Petrel Seismic to Simulation Software database. The same software will be used in construction of regional 3D structural depth model that will be used for determination of fault properties including geometry, time of activity, amplitudes of vertical displacement, and fault rupture parameters. Calculated fault rupture parameters will be used in assessment of fault seismogenic potential trough computation of earthquake magnitudes and possible vertical displacement values during single co-seismic slip using scaling relations (e.g. Wells and Coppersmith, 1994). Validity of constructed geological cross-sections, 3D structural depth model of study area, related fault kinematics and stresses will be also cross-checked with the “Move” Midland Valley modelling software, which we obtained through Academic Software Initiative by Midland Valley, UK). Ii is a software package enabling 2D balanced cross-section construction and 3D model building as the base for the specialist in kinematic, fracture, and sediment modelling and stress analysis. In this way we plan to build geometrically valid geological model which might highlight the timing and significance of critical geological and tectonic events resulting in the formation of the Mt. Velebit area. This result might help to critically re-evaluate all available models proposed for the area.
Calculation of paleo-stress fields based on structural measurements on faults and shear joints will be performed by the WinTensor software of Damien Delvaux that is frequently in use for fault-kinematic analysis and tectonic stress tensor inversion.

 Pristupačnost
Pristupačnost