Ante Ravlić i Nils Paar s Fizičkog odsjeka PMF-a, zajedno sa suradnicima sa sveučilišta u Istanbulu, Lanzhou, Milanu i Orsayu, objavili su u međunarodnom časopisu Physical Review C rezultate istraživanja procesa uhvata elektrona u jezgrama u uvjetima koji prevladavaju u unutrašnjosti zvijezda sa kolapsirajućom sredicom koje mogu završiti eksplozijom supernove.
Istraživanje uhvata elektrona u jezgrama je od iznimne važnosti za proučavanje dinamike razvoja zvijezda sa kolapsirajućom sredicom koje mogu završiti eksplozijom supernove. To je još 1981. pokazao H. Bethe zajedno sa suradnicima u [H. Bethe, G. Brown, J. Applegate, and J. Lattimer, Nucl. Phys.A 324, 487 (1979).] gdje je demonstrirano da dinamika ovisi o dva parametra: omjeru broja elektrona i bariona $Y_e$ te entropiji sredice. Reakcijom uhvata elektrona smanjuje se raspoloživi broj elektrona u sredici zvijezde, a time i $Y_e$ dok izlazni neutrini smanjuju entropiju sredice. Sredica masivne zvijezde je u ravnoteži između tlaka plina degeneriranih elektrona i gravitacijskog privlačenja sve dok njezina masa ne dosegne kritičnu Chandrasekharovu masu $M_{ch}$, tada tlak više ne može zadržati gravitacijsku silu i sredica kolapsira.
Brojna istraživanja tijekom zadnjih 40ak godina bila su posvećena određivanju udarnih presjeka i stopa reakcije uhvata elektrona počevši još od razvoja formalizma uhvata elektrona u zvjezdanom mediju Fullera, Fowlera i Newmanna koji su objavili seriju radova sa tabeliranim proračunima reakcija slabom silom [G. M. Fuller, W. A. Fowler, and M. J. Newman, Astrophys. J. Suppl. Ser. 42, 447 (1980).].
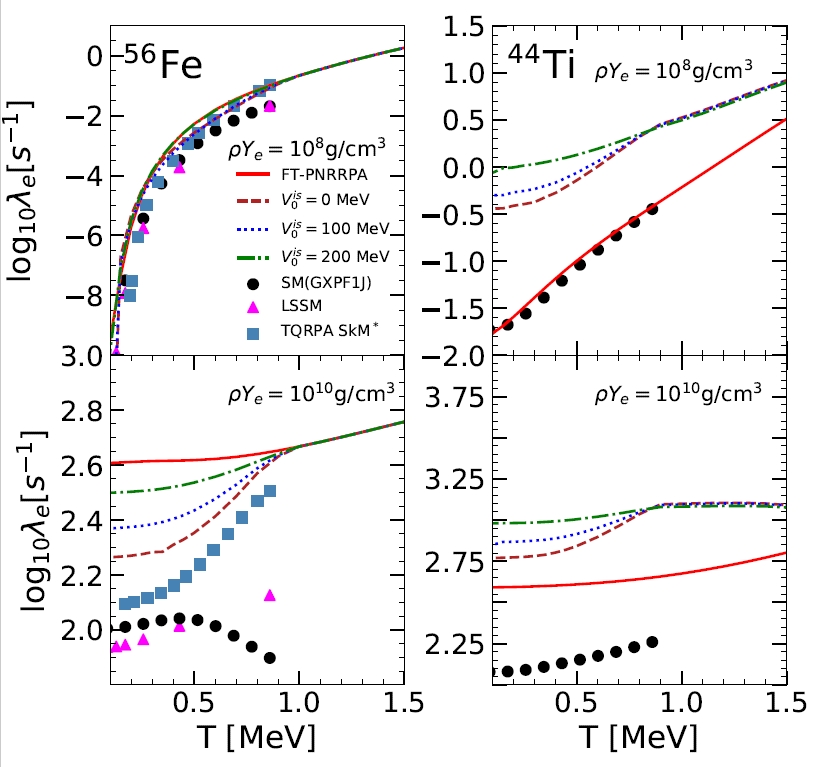
U ovom radu demonstrirali smo izračun stopa uhvata elektrona na jezgrama 44Ti i 56Fe u okviru relativističkog funkcionala gustoće. Za opis osnovnog stanja jezgre koristili smo Hartree-Bardeen–Cooper–Schrieffer teoriju na konačnoj temperaturi (FT-HBCS), a za izračun pobuđenih stanja relativističku kvazičestičnu aproksimaciju slučajne faze na konačnoj temperaturi u proton-neutron bazi (FT-PNRQRPA) koristeći DD-ME2 interakciju [E. Yüksel, N. Paar, G. Colò, E. Khan, and Y. F. Niu, Phys.
Rev. C 101, 044305 (2020).]. Naši izračuni predstavljaju prve izračune stopa uhvata elektrona na konačnoj temperaturi uključujući interakciju sparivanja u osnovom stanju i pobuđenim stanjima jezgre na samosuglasan način. S obzirom na sačuvanje kvantnih brojeva interakcija sparivanja se može podijeliti na izovektorsku i izoskalarnu. Dok je izovektorska interakcija već odavno dobro određena iz eksperimentalnih podataka, izoskalarna nije [C. L. Bai, H. Sagawa, G. Colò, Y. Fujita, H. Q. Zhang, X. Z. Zhang, and F. R. Xu, Phys. Rev. C 90, 054335 (2014).] te su potrebna dodatna istraživanja u ovom smjeru. Stoga smo u ovom radu proučavali kako reakcija uhvata elektrona ovisi o snazi izoskalarne interakcije sparivanja. Primjer takvog rezultata je demonstriran na priloženoj slici gdje je prikazan logaritam stopa uhvata u ovisnosti o temperaturi u intervalu T = 0 - 1.5 MeV za 56Fe (lijevo) i 44Ti (desno) pri gustoćama $\rho Y_e = 10^8$ g/cm${}^3$ i $\rho Y_e = 10^{10}$ g/cm${}^3$. Odabrani parametri simuliraju uvjete koji se nalaze u supernovi sa kolapsirajućom sredicom. Crvena puna linija na slici predstavlja FT-RRPA račun [Y. F. Niu, N. Paar, D. Vretenar, and J. Meng, Phys. Rev. C 83,045807 (2011).] koji ne uključuje interakciju sparivanja pa zaključujemo da interakcija sparivanja može dovesti do promjene od nekoliko redova veličine kod stopa uhvata. Također, značajan utjecaj dolazi od izoskalarne interakcije sparivanja koju smo u ovom radu varirali unutar intervala $V^{is}=0-200$ MeV.
Ovo istraživanje i implementacija novih metoda vodi na mogućnost proračuna stopa uhvata elektrona duž karte nuklida, što se onda može koristiti za analizu njihovih utjecaja na dinamiku supernovi sa kolapsirajućom sredicom. Trenutno radimo na jednom takvom istraživanju u suradnji sa kolegama na Michigan State University (MSU).
Više pojedinosti u članku:
A. Ravlić, E. Yuksel, Y. F. Niu, G. Colo, E. Khan, and N. Paar, Stellar electron-capture rates based on finite-temperature relativistic quasiparticle random-phase approximation, Physical Review C 102, 065804 (2020).
Link na članak: https://journals.aps.org/prc/abstract/10.1103/PhysRevC.102.065804
Link na članak arxiv: https://arxiv.org/abs/2006.08803