U nedavno objavljenom znanstvenom radu u časopisu Physical Review Letters, znanstvenici Dario Jukić, Frane Lunić i Hrvoje Buljan sa Sveučilišta u Zagrebu (dvojica s PMF-a) objavili su članak naslovljen Dynamically Emerging Topological Phase Transitions in Nonlinear Interacting Soliton Lattices.
Solitoni su valovi samotnjaci koji u disperzivnom i nelinearnom mediju putuju na način da ne mijenjaju oblik. Rezultat su savršene ravnoteže između nelinearnosti i disperzije. Jedno od njima karakterističnih svojstava jest da im se oblik čuva i u sudarima solitona. To svojstvo omogućuje stvaranje međudjelujućih solitonskih rešetki koje dinamički evoluiraju, a da pri tome zadržavaju neke od karakteristika samih rešetki.
U ovom radu teorijski je analizirana nelinearna fotonička Su-Schrieffer-Heeger (SSH) rešetka koja se dinamički mijenja i prolazi topološke fazne prijelaze. SSH rešetka naime može biti u dvije različite topološke faze, a netrivijalnu topologiju omogućuje kiralna simetrija rešetke. U trivijalnoj topološkoj fazi ima dvije vrpce, a takozvana Zakova faza koja opisuje namatanje Blochovih valnih funkcija u Brillouinovoj zoni je nula. U netrivijalnoj fazi, Zakova faza iznosi π tj. valne se funkcije netrivijalno namataju. Ta je topološka invarijanta povezana sa postojanjem topoloških rubnih stanja koja su energije jednake nuli. Dinamički topološki fazni prijelaz je karakteriziran sa zatvaranjem procijepa i izranjanjem lokaliziranih stanja iz vrpci u procjep.
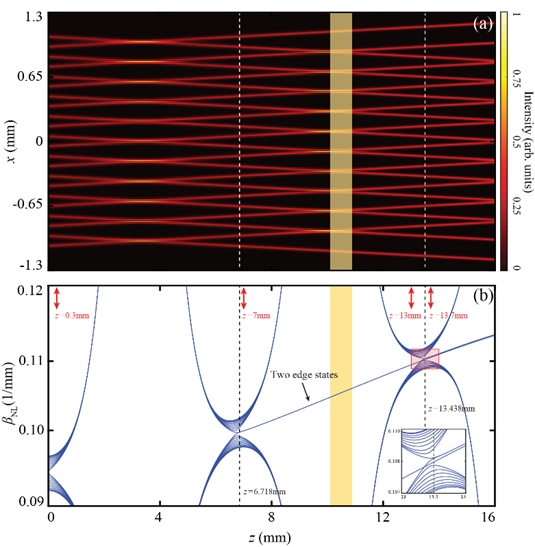
Na slici je prikazana evolucija rešetki u realnom prostoru kao i evolucija spektra na kojem su označena mjesta faznih prijelaza.
Poveznica je ovdje: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.184101